

某商场从一批袋装食品中随机抽取10袋,测得每袋重量(单位:克)分别为789.780,794,762,802,813,770,785,810,806,假设重量服从正态分布,要求在5%的显著性水平下,检验这批食品平均每袋重量是否为800克。
根据上述资料请回答:
提出原假设与备择假设为()。
H0:μ=800; H1:μ≠800
H0:μ=800;H1:μ>800
H0:μ=800; H1:μ<800
H0:μ≠800;H1:μ=800
由于只关心平均重量是否为800克,故采用双侧检验,即H0:μ=800; H1:μ≠ 800。
选择的检验统计量是()。
总体方差未知,故选取t统计量,即![]()
假设检验的拒绝域是()。
(- ∞,-zα/2]∪[zα/2, +∞)
(- ∞,-tα/2]∪[tα/2, +∞), tα/2= tα/2(n)
(- ∞,-tα/2]∪[tα/2, +∞), tα/2= tα/2(n-1)
( tα,+∞)
总体服从正态分布,总体方差未知时,构造t统计量:![]()
(-∞,- tα/2] ∪[tα/2,+∞),tα/2= tα/2(n-1)
假设检验的结论为()。
在5%的显著性水平下,这批食品平均每袋重量不是800克
在5%的显著性水平下,这批食品平均每袋重量是800克
在5%的显著性水平下,无法检验这批食品平均每袋重量是否为800克
这批食品平均每袋重量一定不是800克
假设检验步骤为:
①提出假设:H0:μ=800;H1:μ≠800;
②由于σ2未知,故选择检验统计量为:
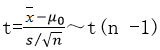
③由α =0.05,查t分布表得临界值:
tα/2= tα/2(n-1)=t0.025(10 -1)=t0.025 (9) =2.2622
拒绝域为:(- ∞,-tα/2]∪[tα/2, +∞),即(-∞,-2.2622] ∪[2.2622,+∞);
④计算统计量观测值t:
![]()
⑤作出统计判断:
因为|t|=1.642<2.2622,所以当α=0.05时,接受H0,即在5%的显著性水平下,这批食品平均每袋重量是800克。